数学领域大名鼎鼎的克莱因瓶虽发现已经一个多世纪，但其瓶颈与瓶壁的相交状态始终没有实质性改变。但近日胡志立受到自己原创的《一种拓扑学教学用具》专利模型地启发，联想到将其与克莱因瓶较好地融为一体，并打造出一款升级版的克莱因瓶模型，暂称耦合式克莱因瓶或叠加态克莱因瓶，胡志立认为它是解决克莱因瓶瓶颈与瓶壁相交问题的较好模型和方案，因此在此基本上实锤了四维空间甚至是更高维空间的存在。

克莱因瓶是什么?

克莱因瓶在数学领域中是指一种无定向性的平面，比如二维平面，就没有内部和外部之分，克莱因瓶在拓扑学中是一个不可定向的拓扑空间，克莱因瓶最初由德国几何学家菲利克斯·克莱因 (Felix Klein) 提出，数学家菲利克斯·克莱因在1882年发现了后来以他的名字命名的瓶子，克莱因瓶的结构可表述为：一个瓶子底部有一个洞，现在延长瓶子的颈部，并且扭曲地进入瓶子内部，然后和底部的洞相连接，和我们平时用来喝水的杯子不一样，这个物体没有边，它的表面不会终结，它和球面不同 ，一只苍蝇可以从瓶子的内部直接飞到外部而不用穿过表面，即它没有内外之分。

克莱因瓶这个名字的翻译其实是有些错误的，因为起初用德语命名时名字中“Kleinsche Fläche”是克莱因平面的意思，因为翻译问题写成了Flasche，这个词才是瓶子的意思，不过不要紧，瓶子这个词用起来也很合适。

克莱因瓶是一个像球面那样封闭的，也就是说没有边的曲面，但是它却只有一个面，在图片上我们看到，克莱因瓶的确就像是一个瓶子，但是它没有瓶底，它的瓶颈被拉长，然后似乎是穿过了瓶壁再和瓶子底部的洞连接在一起的. 如果瓶颈不穿过瓶壁而从另一边和瓶子底部的洞连接的话，我们就会得到一个环面。

克莱因瓶是一个不可定向的二维紧流形，而球面或轮胎面是可定向的二维紧流形，如果观察克莱因瓶，有一点似乎令人困惑--克莱因瓶的瓶颈和瓶身是相交的，换句话说，瓶颈上的某些点和瓶壁上的某些点占据了三维空间中的同一个位置。

克莱因瓶成证明高维空间存在关键

克莱因平面，即克莱因瓶或常规克莱因瓶，克莱因瓶的瓶颈与瓶壁直接相交状态、被认为是在我们这个三维世界想要表达四维世界样貌的无奈和将就之举，而真正理想的克莱因瓶其瓶颈并不会直接穿过瓶壁，而是会通过空间的第四维度避开瓶壁间接穿过，所以人们推断，现实世界只要找到了能够使克莱因瓶瓶颈避开瓶壁而穿过的方式，即只要解决了克莱因瓶的这个痛点，就算证实了四维空间甚至是更高维空间的存在。

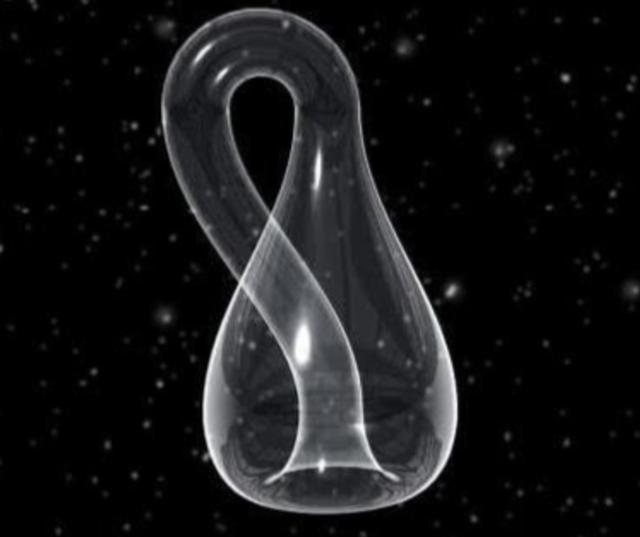
克莱因瓶在四维空间中的理解

我们可以把克莱因瓶放在四维空间中理解：克莱因瓶是一个在四维空间中才可能真正表现出来的曲面，如果我们一定要把它表现在我们生活的三维空间中，我们只好将就点，把它表现得似乎是自己和自己相交一样，理想克莱因瓶的瓶颈是穿过了第四维度才和瓶底洞口连接起来的，并不穿过瓶壁，用纽结来打比方，如果把它看作平面上的曲线的话，那么它似乎自身相交，再一看似乎又断成了三截，但其实很容易明白，这个图形其实是三维空间中的曲线，它并不和自己相交，而是连续不断的一条曲线，在平面上一条曲线自然做不到这样，但是如果有第三维的话，它就可以穿过第三维来避开和自己相交，只是因为我们要把它画在二维平面上时，只好将就一点，把它画成相交或者断裂了的样子，克莱因瓶也一样，我们可以把它理解成处于四维空间中的曲面，在我们这个三维空间中，即使是高明的能工巧匠，也不得不把它做成自身相交的模样;就好像高明的画家，在纸上画纽结的时候也不得不把它们画成自身相交的模样。

最后我们给出克莱因瓶定义。克莱因瓶定义为正方形区域 [0,1]×[0,1] 模掉等价关系(0,y)~(1,y), 0≤y≤1 和 (x,0)~(1-x,1), 0≤x≤1，类似于 Mobius Band, 克莱因瓶不可定向，并且克莱因瓶只能嵌入四维(或更高维)空间。

耦合式克莱因瓶问世证实四维及高维空间的存在

设想将“隐纽结拓扑球”嵌在“克莱因瓶”的瓶颈和瓶身相交位置，使得两个独立拓扑模型混合统一为一种新模型，即所谓的“耦合式克莱因瓶”或“耦合式克莱因平面”，此设想无疑达到了使常规“克莱因瓶”瓶颈和瓶壁避开直接相交的目的，从而证实四维甚至是更高维空间的存在，这部分主要研究这个问题 。

“隐纽结拓扑球”即“隐纽结闭曲面”，如图所示，外观呈立体球形，中间贯穿了一条纽结孔洞，孔洞不能有任何一处触碰粘连点，且孔洞两端出口均呈喇叭口状，因为纽结本身具有手性特征，所以“隐纽结拓扑球”同样也具有手性特征，另外从它的拓扑性质上来看，它仍然属于一种有内外之分的可定向性闭合曲面，实际上也可以把“隐纽结拓扑球”当成“另类克莱因瓶”来看待，其特点是壁面不存在自己与自己“丁”字交叉状态，痛点是其仍属于可定向性性质，这恰恰和克莱因瓶的性质截然相反，所以把它们相互耦合在一起，虽不能解决“隐纽结拓扑球”的定向性问题，但解决了克莱因瓶瓶颈直接穿壁问题，另外还须強调说明，“隐纽结拓扑球”模型可以被制造出来，而且现在也已经被制造出来。下面图中1是球体，2是打结形孔洞。

由于新模型制造比较困难，内部打结部分不是很透明，所以其实克莱因瓶瓶颈不但变长了而且也打结了，这些都是为了弥补模型的缺陷。

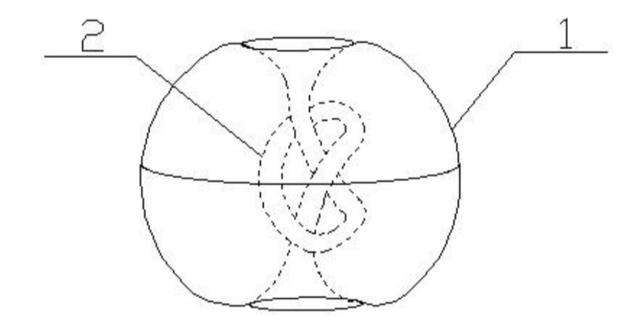
耦合式克莱因瓶就是由图所示的一种“隐纽结拓扑球”模型、嵌设于上图中所示的常规“克来因瓶”瓶颈与瓶壁相交位置，得到的一种混合态克莱因瓶模型，此设想是一次大胆地尝试，它将常规“克莱因瓶”的瓶颈与瓶壁直接相交状态改为间接相交状态，研究认为这是避免“克莱因平面”自身相交的较优方式，并且由于“隐纽结拓扑球”自身隐纽结所具有的手性特征，也使得耦合式克莱因瓶同样也有了手性特征，另外有了兼容组合的思维观念，我们甚至还会想到由多个或上万个“克莱因瓶”、和上万个“隐纽结拓扑球”共同组合而成的超级耦合式克莱因瓶模型。

免责声明：市场有风险，选择需谨慎！此文仅供参考，不作买卖依据。

责任编辑：kj005